Found Music
Samuel Vriezen’s liner notes from Ensemble Klang’s recording of Tom Johnson’s works Cows, Chords & Combinations (EKR02).
‘Finding’ your work of art instead of having to ‘create’ it may seem easy, until you recognize that not everything that exists can be created by humans, yet everything we know was at some point ‘found’. Mathematics, for example, is often thought of by its practitioners as something ‘found’; and indeed no-one could ever hope to think up something so infinitely mysterious and complex as, say, the prime numbers, which have kept mathematicians enthralled from the dawn of science to the present day. Thus, the things we can ‘find’ exceed the things we may ‘create’. That makes ‘finding’ not at all trivial.
Tom Johnson is a vocal supporter of the idea of ‘finding’ works of art. This makes him part of a rich, by now venerable, tradition in experimental art of artists who prefer finding to creating. In each case the act itself of ‘finding’ seems similar but since there are so many different things to be ‘found’ the results are diverse indeed: there is Marcel Duchamp finding obscure erotic meanings in banal objects, John Cage finding beauty in pure chance, or the poet Kenneth Goldsmith finding unreadability in a perfectly normal copy of the New York Times simply by transcribing it as a 900 page book. In Johnson’s case, a surprising beauty is found in the regularity, logic and symmetry of pre-existing mathematical structures, which are translated into musically audible forms.
Intuition, clarity & metaphysics
With his musical formation coming in the experimental scene of 1960s New York, Johnson has often named John Cage and his teacher Morton Feldman as important influences. Johnson follows Cage in subscribing to the ideal of non-intentionality: the artist should strive to submit the details of his work of art as little as possible to the whims of personal taste and as much as possible to disciplining forces outside of himself; hence the idea of ‘finding’ music. From Feldman, he learnt that composing is about listening for where the sound wants to go. In Feldman’s work, that attitude leads to an intuitive sense of form, almost as if the form is improvised from sound to sound, which may seem incompatible with Cage’s notion of being subjected to external discipline. Indeed, Johnson’s earliest pieces do not yet feature the rigorous structures of his mature work, but already in a piece like Spaces for piano (1969) you can hear a clarity of texture, an ear for transparent harmony and a preference for simple and elegant rhythmical structures that have remained characteristic features of his music.
 844 Chords, performed at the Orgelpark, Amsterdam
844 Chords, performed at the Orgelpark, Amsterdam
Gradually, Johnson would abandon the more intuitive forms. In his mature works, clarity, transparency and simplicity become more than mere characteristics of his sound world and develop into structural determinants that drive the forms themselves. It is as if Johnson had been listening to his sounds and discovered that what they wanted to do first of all was to be clear, and therefore to be submitted to an audible logic. Regularity, rationality and predictability took on a new importance, as shown by provocatively titled pieces such as Predictables for piano trio (1984) and Rational Melodies (1982). And it was this drive towards logic that sparked his interest in the use of mathematical structures as found objects, and that made him study a great variety of mathematical subjects, including group theory, cellular automata, the theory of tilings and combinatorics.
“you can often hear the sheer pleasure musicians have when playing his work”
Having come to this point, Johnson’s music began to exist on two levels simultaneously. There is the level of the structural idea, which is often very clear and in principle predictable; and there is the physical level of the sounds and the playing. Johnson himself writes in Music Metaphysics (2004): “I am not interested in the esthetics of my music, but rather in its metaphysics. Esthetics has to do with beauty, sounds, appearances, while metaphysics has to do with the essence of the music: where did it come from, how did it make itself, why is it there?” However, an important part of what makes listening to many pieces by Johnson such an enjoyable experience is precisely the way that these two levels do play off against one another and create a new space for the listener.
The music of predictability: Rational Melodies
In most music, you’re simply following what is happening and the pleasure comes from being immersed or being drawn along by the flow of the music. This is certainly true for the kind of gesture-based neo-expressionist music that still seems to dominate the contemporary music field today, in which unpredictability is an essential part of expression, but it’s also true for trance-inducing types of minimal music. Johnson’s music, too, can be rewarding when listened to at this level, since his work always sounds attractive and musical, full of harmonic beauty and melodic vitality. Because the music is so transparent musicians must always take great care in their articulation and phrasing or even, as shown by Klang’s performances of the Rational Melodies on this disc, their choice of instrumentation. This makes performing Johnson’s music challenging, fun and rewarding, and you can often hear the sheer pleasure musicians have when playing his work.
 The opening of Rational Melody XII by Tom Johnson
The opening of Rational Melody XII by Tom Johnson
But at the same time the clarity of the idea invites you to think along with the music. In most of the Rational Melodies, it is in principle possible to predict how a melody is going to develop after the first couple of bars. It’s hardly possible to imagine a simpler idea than that of, say, Rational Melody XII, in which a repeated sequence of descending fifths gradually turns into a descending chromatic scale. By bar eight you should be able to hum along, or at least get the idea and listen to this idea unfold exactly as expected. To borrow some terminology from that other great composer with a serious interest in mathematics, Iannis Xenakis, this means that now you can not only appreciate the music “in-time”, enjoy the pleasure of being present as it unfolds, but also “outside-time”: you can enjoy the concept of the overall structure. Your attention as a listener can also now go back and forth between these levels, and you can appreciate how the concept determines the details of what you hear and vice versa. This means that listening becomes a more conscious activity, and a matter of choosing on what level you listen, of how you listen and what you listen for. And so, as the listener is consciously confronted with his own listening, listening becomes self-reflective. In this way, the conceptual rigour of the music opens up a new space for listening as active participation rather than passive pursuit.
 Tom Johnson & Ensemble Klang at the recording sessions for the album Cows, Chords & Combinations in 2009
Tom Johnson & Ensemble Klang at the recording sessions for the album Cows, Chords & Combinations in 2009
A lecture on growth: Narayana's Cows
In many works, Johnson has used the medium of text to underscore this self-reflective aspect of his music. In the piece Music and Questions for a speaker playing five bells (1988), a sequence of predictable musical phrases alternate with questions about listening to the music – and to the questions. Elsewhere it takes an openly didactic form and the pieces become lecture-performances, with a speaker explaining the structure of the music and the mathematics behind it as the music unfolds. A great example of that technique is Narayana’s Cows (1989), one of Johnson’s most popular works, which is a demonstration of a 14th century Indian mathematics problem about the growth of a herd of cows. A fascinating aspect of pieces like Narayana’s Cows is the elegant way in which talking gives way smoothly to pure music. First you’re listening to a lecture on mathematics with examples in sound, then, after a while, you suddenly realize it is actually music that you are listening to. In this case, with each generation, the musical phrases get longer as Narayana’s herd grows larger, and so generation by generation the music becomes more important than the talk.
“the greatest pleasure may simply lie in the richness and variety of the chords themselves”
Because of the nested structure of the phrases in Narayana’s Cows, it may be harder for a listener to accurately predict how the piece will develop than in the Rational Melodies. When Johnson turns his attention to logical progressions of chords in works such as the famous Chord Catalogue (1985), the music often gets even more difficult to predict, though you can sense that there is a strong logic and feel where the music is going – a process that happens in a single voice will be easier to grasp than a process that is played out polyphonically. But there is more to it. Harmonic structures can not always be best expressed in linear fashion, the way melodic structures almost by definition are. The two most recent works on this disc show two very different approaches that Johnson has been developing for rationally organizing chord sequences; the difference between the two approaches in fact signals a new direction in Johnson’s basic esthetic concerns that has emerged in some of his most recent work.
Arithmetic Sensuality: 844 Chords
844 Chords (2005), subtitled “Rational Harmonies in Five Voices”, represents the older approach. It is a chord enumeration piece that goes through all possible five-part chords that encompass at least 18 semitones and at most 31 semitones, with never more than an octave between neighbouring voices and never less than a tritone between the lowest and second lowest voices, never less than a fourth between the second lowest and middle voices, never less than a major third between the middle and second highest voices and never less than a minor third between the second highest and highest voices. These chords unfold in a logical but slightly complicated order. It is, however, possible to sense the process in a few ways. Most clearly, the bass voice descends very gradually as the width of the chords slowly expands semitone by semitone over the course of the piece, but additionally the enumeration strategy leads to a patterned phrasing structure that is most clearly heard by listening to the second voice, which consists mostly of rising chromatic lines. (The second voice is in fact the leading melody voice; the top voice exclusively plays the note D all through the piece). You can hear these chromatic lines gradually expand and contract in length. However, the greatest pleasure of the piece may simply lie in the richness and variety of the chords themselves, which can be surprisingly suggestive. As Johnson himself writes, “Sometimes one even hears reappearances of chromatic harmonies from the era of Franck and Wagner, though their sensuality is essentially arithmetic rather than emotional, and their score is a simple Mathematica program!”
 Opening page of the score of 844 Chords by Tom Johnson
Opening page of the score of 844 Chords by Tom Johnson
A mysterious order: Vermont Rhythms
The newer approach is exemplified on this disc by Vermont Rhythms (2009). The point of departure for this piece was not harmony as such but rhythmical possibilities: the composition is an enumeration of all 462 possible 6-note rhythms that exist with each of the six notes being assigned to one of 11 beats (the piece is in 3/2 time and the 11 beats are the first 11 eighth note positions, so the last eighth of any bar is always excluded from the rhythmical phrase). However, the way these rhythms are presented makes use of ideas out of combinatorial mathematics, involving structures that are known as “block designs”, which Johnson first began to investigate for their possibilities in harmony – and in fact, the chord structure of Vermont Rhythms is determined by the same idea.
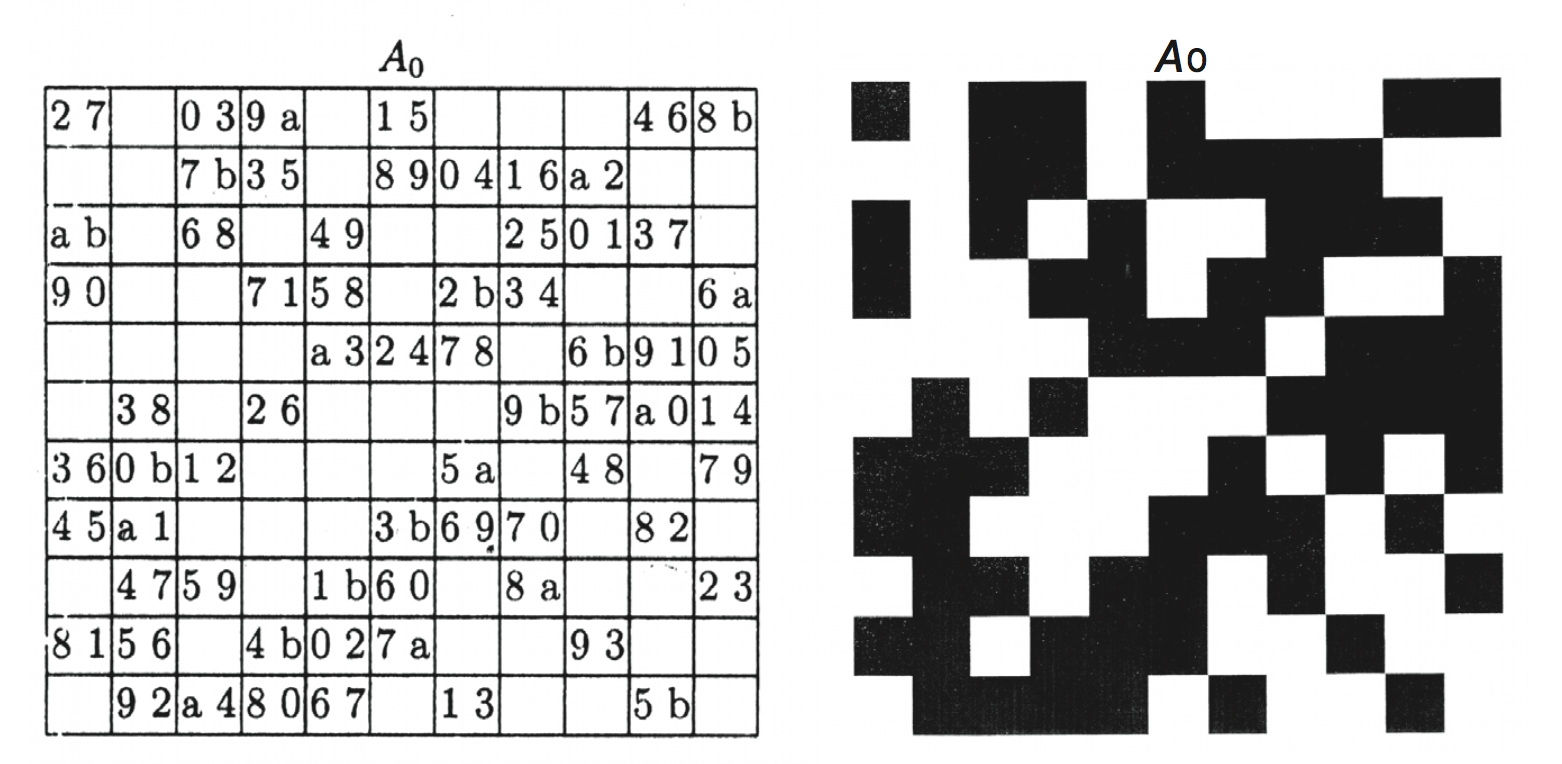
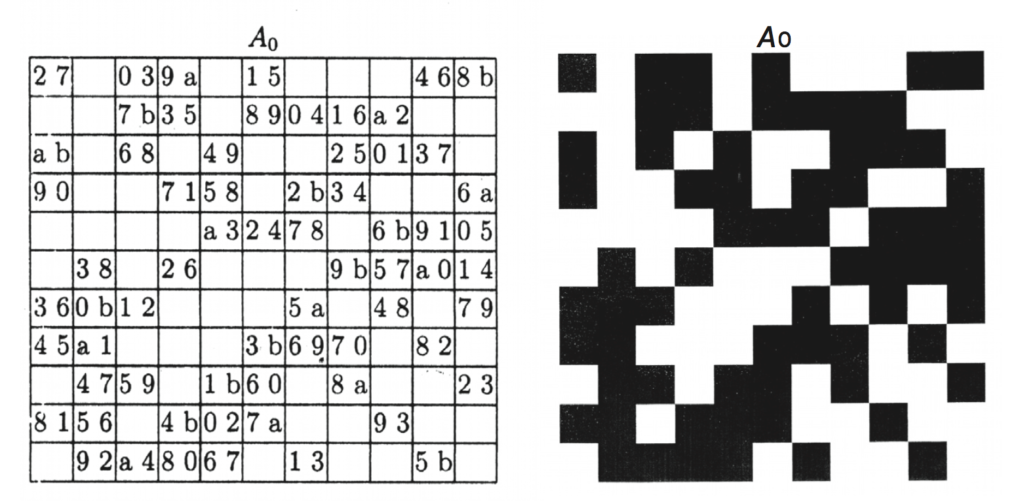 Above left, the first of the 42 individual 11x11 squares calculated by Susan Janiszewski and Jeffrey H. Dinitz for Tom Johnson's Vermont Rhythms. Above right, the same square drawn by Tom Johnson, in which you can see each horizontal row and each vertical column containing 6 filled squares.
Above left, the first of the 42 individual 11x11 squares calculated by Susan Janiszewski and Jeffrey H. Dinitz for Tom Johnson's Vermont Rhythms. Above right, the same square drawn by Tom Johnson, in which you can see each horizontal row and each vertical column containing 6 filled squares.
In 2003, Johnson came across these fascinating mathematical structures – in fact, it was the writer of these liner notes who brought them to his attention. In a few pieces that I had written in 2002, I had used collections of chords, every pair of which would have exactly the same number of pitches in common, so that every chord from the collection related to every other chord in the collection in exactly the same way – an extraordinary symmetry feature that is typical of block designs. When I mentioned this to him, Johnson was very interested. Before long he had studied the field of block design theory much more profoundly than I had, and was starting to look for new musical applications. Here he showed himself true to his ideal of found structure. If for me the block design structure had been a solution for just an aspect of some piece, for Johnson they were found objects to be translated into music, and the compositional problem came only after the find: how does one best audibly clarify the extraordinarily rich symmetrical structure of these block designs? This led him to a whole series of pieces entirely based on block designs, from which Vermont Rhythms is a later offshoot.
 Photo collage from world premiere of Vermont Rhythms, at Kettle's Yard, Cambridge (UK), 1 February 2009. (c) On an Overgrown Path
Photo collage from world premiere of Vermont Rhythms, at Kettle's Yard, Cambridge (UK), 1 February 2009. (c) On an Overgrown Path
In one important aspect Johnson’s block design work differs from his earlier work based on logical sequences: block design harmonies consist of collections of chords in which every chord has the same structural role as every other chord. Which means that there no longer exist naturally given logical sequences for presenting them. Instead, there is a balance to the whole of the system, since every pitch appears exactly the same number of times in the collection, and so does every pair of pitches. As a result, Johnson’s music based on these combinatorial structures tends to be less didactic and self-reflexive, and much more static; it becomes almost meditative, inviting contemplation of mysterious orders of complex symmetries, that we may not be able to quite grasp completely as we listen but of which we may have a sense of their presence.
 The opening of Tom Johnson's Vermont Rhythms, with the passage beginning in bar two corresponding to the above squares
The opening of Tom Johnson's Vermont Rhythms, with the passage beginning in bar two corresponding to the above squares
For Vermont Rhythms Johnson asked two mathematicians working at the University of Vermont, Susan Janiszewski and Jeffrey H. Dinitz, to construct a list of the 462 6-note rhythms in a very specific format. The rhythms are listed as 42 groups of 11, and each group of 11 actually is a (11, 6, 3)-design – which means that every one of the 11 beats is used in 6 of the 11 rhythms, and every pair of beats occurs in 3 of the 11 rhythms. The piece expresses each of the groups of 11 rhythms using different instrumentation strategies, so that the instrumentation changes every 11 bars. For the pitches Johnson chose the 462 possible 6-note chords within an 11-note scale, and made their order exactly isomorphic to the order in which the rhythms are presented. So in each 11-bar section (except the ones in which only the percussion is playing) we hear every pitch appear in 6 of the chords, and each pair of pitches in 3 of the chords.
Vermont Rhythms was written especially for Klang, after Johnson had heard the group play Narayana’s Cows during a week devoted to his work in The Hague. Interestingly, Vermont Rhythms has an almost Dutch sound to it, feeling like an hommage to the typical Hague School sound with its fast additive rhythms and loud and dissonant but not quite atonal sounding block chords. Which brings me to a final point about Johnson’s poetics of ‘finding’: its universality. Just as the rigorous patterns of 844 Chords could be surprisingly reminiscent of romantic harmony, here combinatorics naturally leads to an advanced post-Stravinskian sound world. It seems that the mathematical structures that Johnson has been ‘finding’ over the decades have allowed him to cut diagonally across styles and to resist having to bother with stylistic particularism. And so Johnson’s work testifies to the infinite richness of the act of ‘finding’ and of its universal truth. For which being receptive is all it takes.